11.1 The ANOVA F-Test

Now that we understand in what kind of situations ANOVA is used, we are ready to learn how it works.

Stating the Hypotheses

The null hypothesis claims that there is no relationship between \(X\) and \(Y\). Since the relationship is examined by comparing \(\mu_1, \mu_2,\ldots,\mu_k\) (the means of \(Y\) in the populations defined by the values of \(X\)), no relationship would mean that all the means are equal. Therefore the null hypothesis of the F-testis: \(H_0: \mu_1 = \mu_2 = \cdots = \mu_k\).

As we mentioned earlier, here we have just one alternative hypothesis, which claims that there is a relationship between \(X\) and \(Y\). In terms of the means \(\mu_1, \mu_2,\ldots,\mu_k\) it simply says the opposite of the alternative, that not all the means are equal, and we simply write: \(H_a:\) not all the \(\mu\)’s are equal.

Recall our “Is academic frustration related to major?” example:

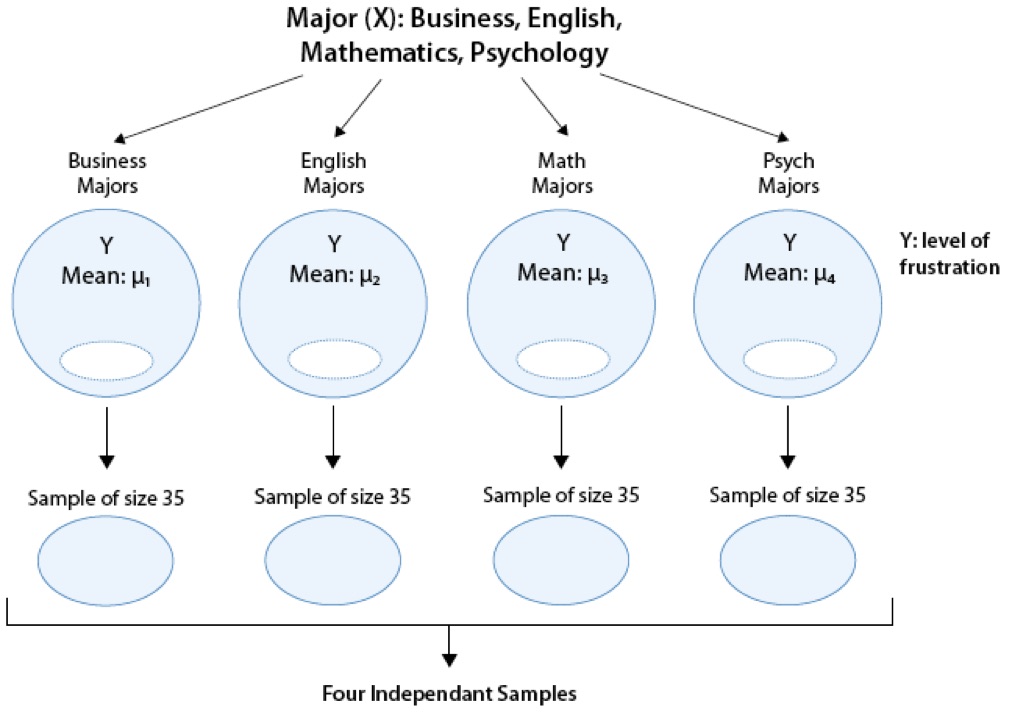
Review: True or False

The hypothesis that are being test in our example are:

\(H_0: \mu_1 = \mu_2 = \mu_3 = \mu_4\)

\(H_1: \mu_1 \neq \mu_2 \neq \mu_3 \neq \mu_4\)

The correct hypotheses for our example are:

\(H_0: \mu_1 = \mu_2 = \mu_3 = \mu_4\)

\(H_1: \mu_i \neq \mu_j\) for some \(i,j\)

Note that there are many ways for \(\mu_1, \mu_2,\mu_3,\mu_4\) not to be all equal, and \(\mu_1 \neq \mu_2 \neq \mu_3 \neq \mu_4\) is just one of them. Another way could be \(\mu_1 = \mu_2 = \mu_3 \neq \mu_4\) or \(\mu_1 = \mu_2 \neq \mu_3 \neq \mu_4\). The alternative of the ANOVA F-test simply states that not all of the means are equal and is not specific about the way in which they are different.