Confidence Interval Simulation Program

This program simulates random samples from which it constructs confidence intervals for either the population mean, the population variance, or the population proportion of successes.

CIsim(samples = 100, n = 30, parameter = 0.5, sigma = 1,
  conf.level = 0.95, type = "Mean")

Arguments

samples	the number of samples desired.
n	the size of each sample.
parameter	If constructing confidence intervals for the population mean or the population variance, parameter is the population mean (i.e., type is one of either "Mean" or "Var"). If constructing confidence intervals for the poulation proportion of successes, the value entered for parameter represents the population proportion of successes (Pi), and as such, must be a number between 0 and 1.
sigma	is the population standard deviation. sigma is not required if confidence intervals are of type "Pi."
conf.level	confidence level for the graphed confidence intervals, restricted to lie between zero and one
type	character string, one of "Mean", "Var", or "Pi", or just the initial letter of each, indicating the type of confidence interval simulation to perform

Value

Graph depicts simulated confidence intervals. The number of confidence intervals that do not contain the parameter of interest are counted and reported in the commands window.

Details

Default is to construct confidence intervals for the population mean. Simulated confidence intervals for the population variance or population proportion of successes are possible by selecting the appropriate value in the type argument.

Examples

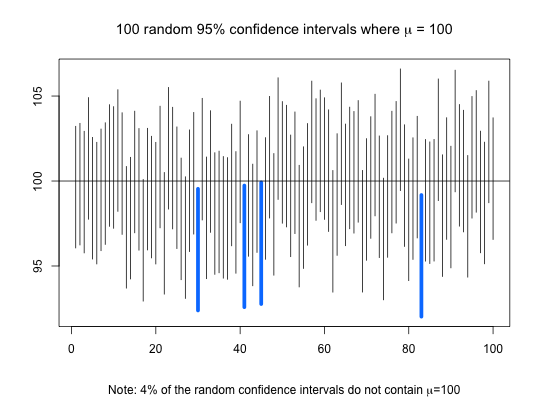
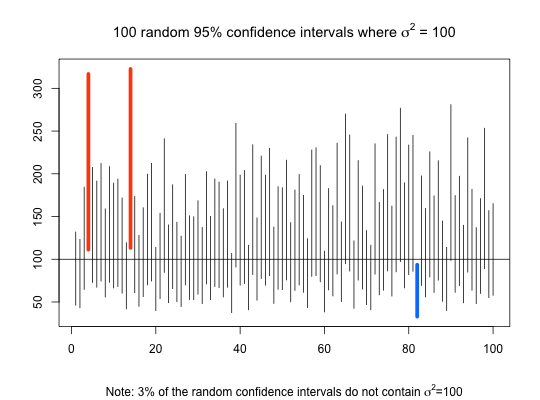
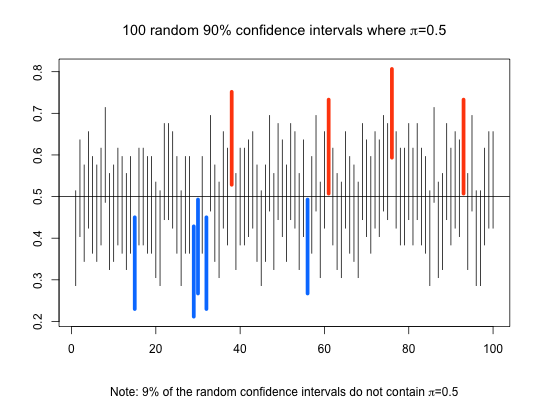
CIsim(100, 30, 100, 10)
#> 4 % of the random confidence intervals do not contain Mu = 100 . 
    # Simulates 100 samples of size 30 from
    # a normal distribution with mean 100
    # and standard deviation 10.  From the
    # 100 simulated samples, 95% confidence
    # intervals for the Mean are constructed
    # and depicted in the graph.

CIsim(100, 30, 100, 10, type="Var")
#> 3 % of the random confidence intervals do not contain Var = 100 . 
    # Simulates 100 samples of size 30 from
    # a normal distribution with mean 100
    # and standard deviation 10.  From the
    # 100 simulated samples, 95% confidence
    # intervals for the variance are constructed
    # and depicted in the graph.

CIsim(100, 50, .5, type="Pi", conf.level=.90)
#> 9 % of the random confidence intervals do not contain Pi = 0.5 . 
    # Simulates 100 samples of size 50 from
    # a binomial distribution where the population
    # proportion of successes is 0.5.  From the
    # 100 simulated samples, 90% confidence
    # intervals for Pi are constructed
    # and depicted in the graph.