Measurements of the thickness of the oxide layer of manufactured integrated circuits

Source: R/BSDA-package.R

Data for Exercises 6.49 and 7.47

Chipavg

Format

A data frame/tibble with 30 observations on three variables

wafer1

thickness of the oxide layer for wafer1

wafer2

thickness of the oxide layer for wafer2

thickness

average thickness of the oxide layer of the eight measurements obtained from each set of two wafers

Source

Yashchin, E. 1995. “Likelihood Ratio Methods for Monitoring Parameters of a Nested Random Effect Model.” Journal of the American Statistical Association, 90, 729-738.

References

Kitchens, L. J. (2003) Basic Statistics and Data Analysis. Pacific Grove, CA: Brooks/Cole, a division of Thomson Learning.

Examples


EDA(Chipavg$thickness)
#> [1] "Chipavg$thickness"

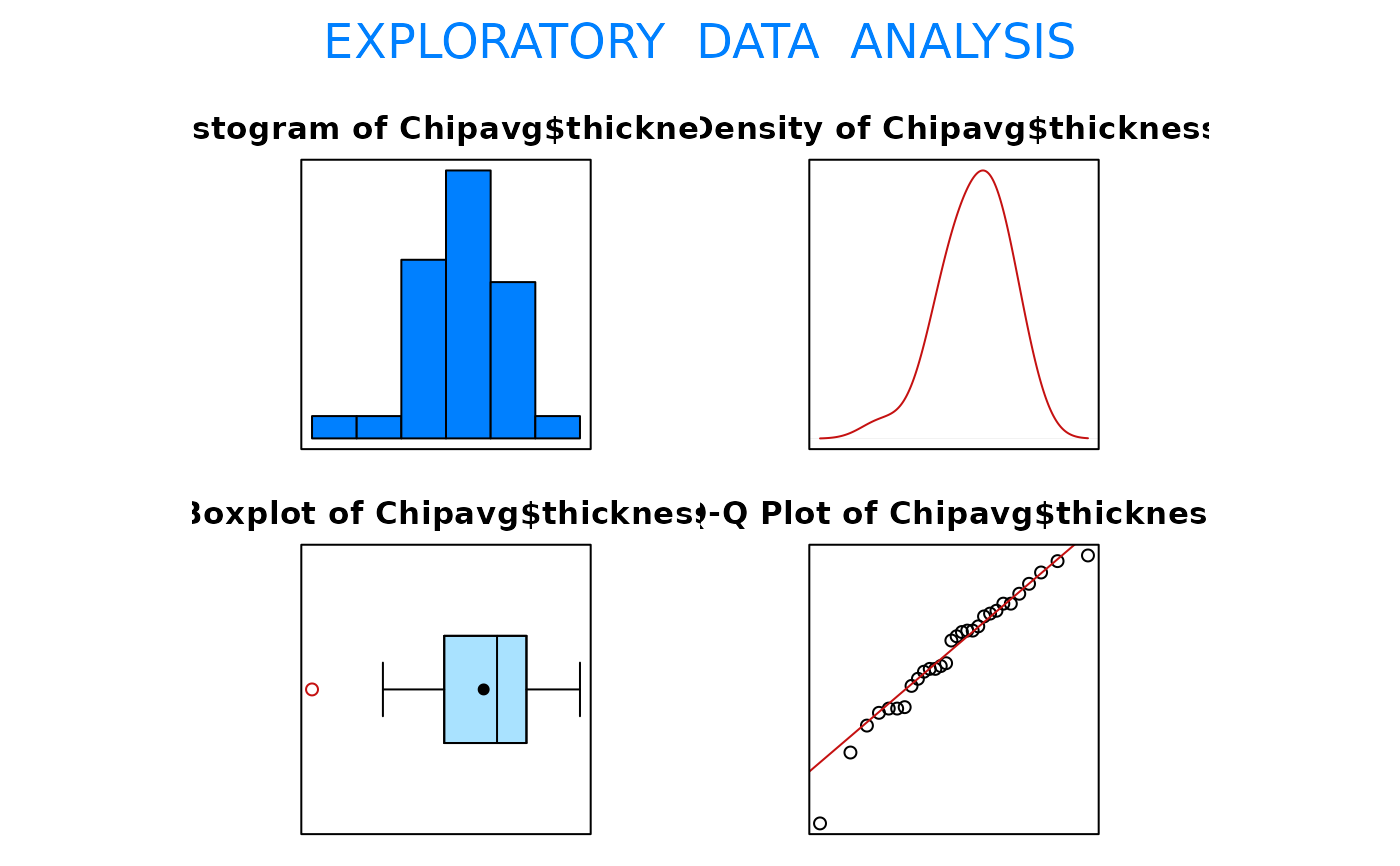#> Size (n)  Missing  Minimum   1st Qu     Mean   Median   TrMean   3rd Qu 
#>   30.000    0.000  865.000  981.562 1016.333 1028.125 1018.705 1054.062 
#>     Max.   Stdev.     Var.  SE Mean   I.Q.R.    Range Kurtosis Skewness 
#> 1101.250   52.954 2804.088    9.668   72.500  236.250    0.308   -0.653 
#> SW p-val 
#>    0.339 
t.test(Chipavg$thickness, mu = 1000)
#> 
#> 	One Sample t-test
#> 
#> data:  Chipavg$thickness
#> t = 1.6894, df = 29, p-value = 0.1019
#> alternative hypothesis: true mean is not equal to 1000
#> 95 percent confidence interval:
#>   996.5601 1036.1065
#> sample estimates:
#> mean of x 
#>  1016.333 
#> 
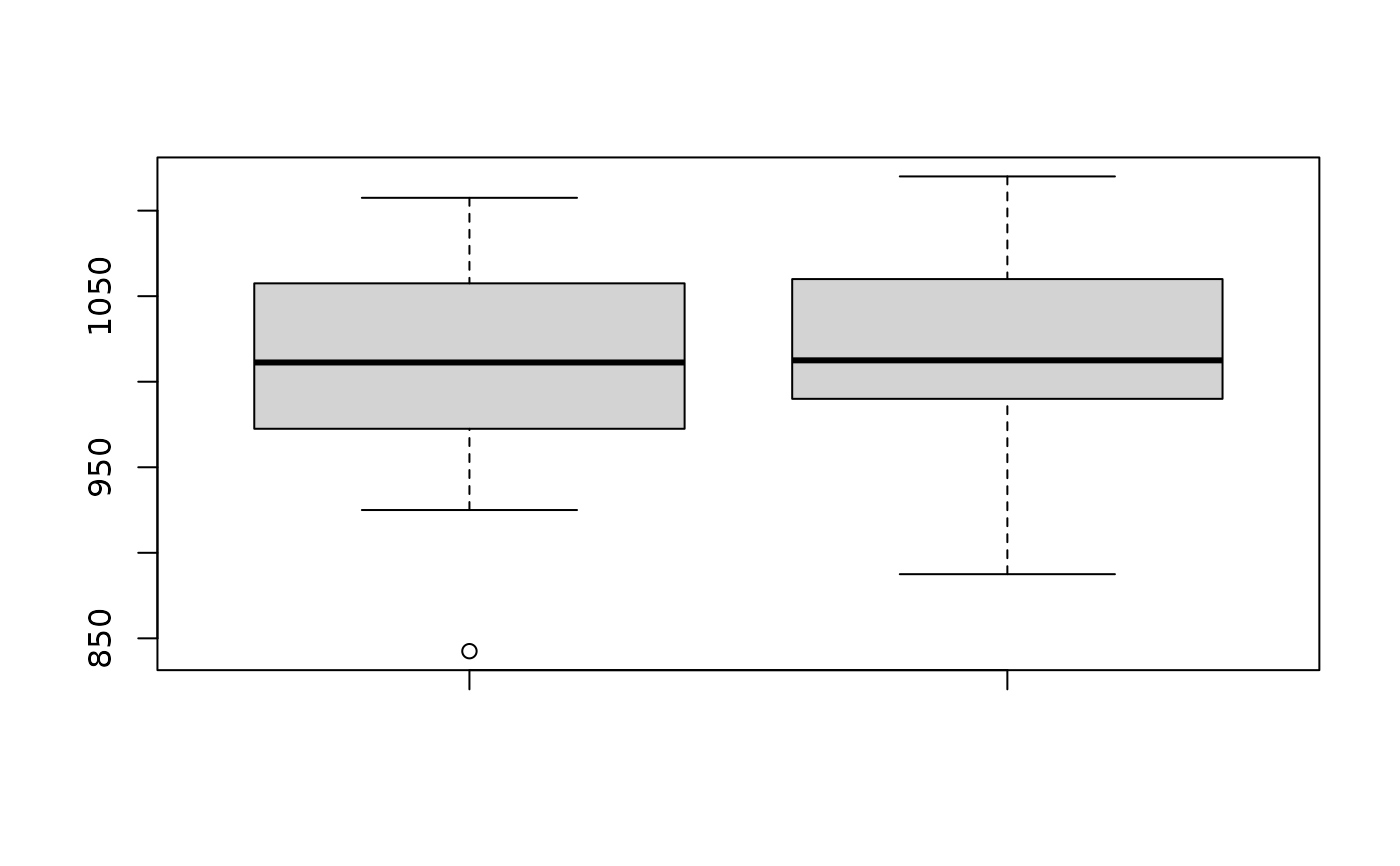
boxplot(Chipavg$wafer1, Chipavg$wafer2, name = c("Wafer 1", "Wafer 2"))

shapiro.test(Chipavg$wafer1)
#> 
#> 	Shapiro-Wilk normality test
#> 
#> data:  Chipavg$wafer1
#> W = 0.9545, p-value = 0.2228
#> 
shapiro.test(Chipavg$wafer2)
#> 
#> 	Shapiro-Wilk normality test
#> 
#> data:  Chipavg$wafer2
#> W = 0.96426, p-value = 0.3959
#> 
t.test(Chipavg$wafer1, Chipavg$wafer2, var.equal = TRUE)
#> 
#> 	Two Sample t-test
#> 
#> data:  Chipavg$wafer1 and Chipavg$wafer2
#> t = -0.55603, df = 58, p-value = 0.5803
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#>  -39.10005  22.10005
#> sample estimates:
#> mean of x mean of y 
#>  1012.083  1020.583 
#>